Математический анализ

"Математический анализ"  является базовым курсом в Институте математики Сибирского федерального университета. Он закладывает фундамент для дальнейшего изучения специализированных математических дисциплин на старших курсах. В расписании вы его можете также встретить под названием "Математический анализ функций действительной переменной". Этот предмет мы с Вами будем изучать на протяжении двух первых курсов (4 семестра). У некоторых групп после третьего семестра предмет превращается в "Дополнительные главы математического анализа".

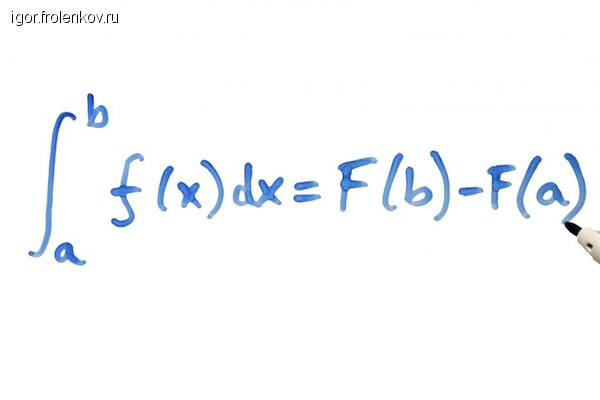Пока Вы изучаете дисциплину, Вам предстоит познакомиться со следующими темами:

1. рассмотрение элементов теории множеств, вещественных чисел, понятий функции и ее графика, изучение пределов последовательности и функции, непрерывности функции;
2. введение понятия производной и дифференциала функции, изучение их свойств и проведение полного исследования функций с помощью производных, рассмотрение обратной операции - интегрирования;
3. введение определенного интеграла Римана и изучение его свойств, определение  и изучение несобственного интеграла, приложение определенного интеграла к вычислению площадей, объемов, длины кривой, площади поверхности и нахождению различных механических и физических величин;
4. рассмотрение понятия сходящегося ряда и суммы ряда, исследование рядов на сходимость и абсолютную сходимость, используя различные признаки. На этой основе изучение функциональных последовательностей и рядов, их равномерной сходимости и ее свойств,  изучение степенных рядов и рядов Фурье;
5. рассмотрение понятия предела, непрерывности функций многих переменных, частных производных и дифференцируемости, приложения дифференциального исчисления к нахождению экстремумов, неявным и обратным функциям, условному экстремуму;
6. введение измеримых по Жордану множеств, внешней и внутренней мер Жордана, изучение классов измеримых множеств. Построение кратного интеграла Римана,  интегральных сумм, сумм Дарбу, изучение критериев интегрируемости, свойств интеграла Римана, интегрируемости непрерывных функций, теоремы Фубини о сведении кратного интеграла к повторному, замене переменных в кратном интеграле.  Построение несобственного кратного  интеграла Римана по неограниченному множеству и от неограниченной функции, получение его свойств, доказательству признаков сходимости;
7. изучение собственных и несобственных интегралов, зависящих от параметра, равномерной сходимости. Рассмотрение приложений данной теории к нахождению различных несобственных интегралов, интегралам Эйлера и интегралу Фурье;
8. рассмотрение понятия криволинейного интеграла первого и второго рода, связи между ними. Введение понятие внешней дифференциальной формы и кусочно-гладкой поверхности. Определение интеграла от дифференциальной формы по цепи и рассмотрение его свойств. Получение основные интегральных формул: абстрактной формулы Стокса, формул Грина, Остроградского, классической формулы Стокса. Изучение элементов векторного анализа (теории поля);
9. обобщенная функция, как линейный и непрерывный функционал; сходимость обобщенных функций, производная обобщенной функции и ее преобразование Фурье.

Что мне нужно знать, чтобы хорошо понимать Математический анализ ?

При изучении математического анализа необходимо знать такие темы алгебры, аналитической геометрии, дискретной математики и математической логики как системы линейных уравнений, векторное и евклидово пространства, матрицы и определители, квадратичные формы, логические символы и операции, комбинаторика, линии второго порядка, поверхности второго порядка.

 
В свою очередь "Математический анализ" является основным при изучении базовых курсов: численные методы, теоретическая механика, дифференциальные уравнения, теория функций комплексного переменного, функциональный анализ, дифференциальная геометрия и топология, теория вероятностей и случайные процессы, а также вариативных курсов: действительный анализ, уравнения с частными производными, математическая статистика, методы оптимизации, математическое моделирование, компьютерная геометрия и геометрическое моделирование, актуарная математика.

Список рекомендуемой литературы по Математическому анализу

Что есть на этом сайте по данной дисциплине?